6: Bisection Methods, Newton/Raphson, Introduction to Lists
def squareRootBi(x, epsilon):
“””Assumes x >= 0 and epsilon > 0
Return y s.t. y * y is within epsilon of x”””
assert x >= 0, ‘x must be non-negative, not’ + str(x)
assert epsilon > 0, ‘epsilon must be positive, not’ + str(epsilon)
low = 0
high = max(x, 1)
guess = (low + high) / 2.0
ctr = 1
while abs(guess ** 2 – x) > epsilon and ctr <= 100:
#print ‘low:’, low, ‘high:’, high, ‘guess:’, guess
if guess ** 2 < x:
low = guess
else:
high = guess
guess = (low + high) / 2.0
ctr += 1
assert ctr <= 100, ‘Iteration count exceeded’
print ‘Bi method. Num. iteratins:’, ctr, ‘Estimate:’, guess
return guessdef squareRootNR(x, epsilon):
“””Assumes x >= 0 and epsilon > 0
Return y s.t. y * y is within epsilon of x”””
assert x >= 0, ‘x must be non-negative, not’ + str(x)
assert epsilon > 0, ‘epsilon must be positive, not’ + str(epsilon)
x = float(x)
guess = x / 2.0
guess = 0.001
diff = guess ** 2 – x
ctr = 1
while abs(diff) > epsilon and ctr <= 100:
#print ‘Error:’, diff, ‘guess:’, guess
guess = guess – diff / (2.0 * guess)
diff = guess ** 2 – x
ctr += 1
assert ctr <= 100, ‘Iteration count exceeded’
print ‘NR method. Num. iterations:’, ctr, ‘Estimate:’, guess
return guesssquareRootBi(9, 0.001)
squareRootBi(4, 0.001)
squareRootBi(2, 0.001)
squareRootBi(0.25, 0.001)
squareRootBi(4, 0.00001)
squareRootNR(4, 0.00001)squareRootBi(123, 0.00001)
squareRootNR(123, 0.00001)squareRootBi(123456789, 0.00001)
squareRootNR(123456789, 0.00001)Techs = [‘MIT’, ‘Cal Tech’]
print TechsIvys = [‘Harvard’, ‘Yale’, ‘Brown’]
print Ivys
Univs = []
Univs.append(Techs)
print Univs
Univs.append(Ivys)
raw_input()
print Univs
raw_input()
for e in Univs:
print e
for c in e:
print c
raw_input()
Univs = Techs + Ivys
print Univs
raw_input()
Ivys.remove(‘Harvard’)
print Univs
Ivys[1] = -1
print IvysL1 = [1, 2, 3]
L2 = L1
L1[0] = 4
print L2
def f(L):
L[0] = 4
L1 = [1, 2, 3]
L2 = [1, 2, 3]
L3 = L1
print L1 == L2
f(L1)
print L1 == L2
print L1
print L2
print L3L1 = [1, 2, 3]
L2 = L1[:] # make a copy of L1
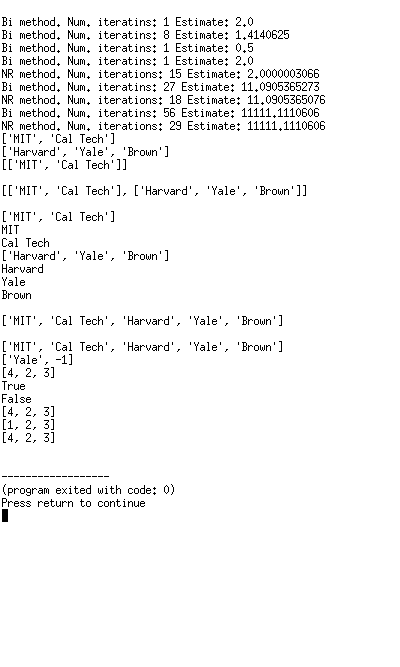
 왜 에러가 뜰까…. 이해가 필요하다..
왜 에러가 뜰까…. 이해가 필요하다..